2.手順と方法
★上記 「1-2 基本ルール」 に基づいて初心者でも難問が解けるように、ナンプレの始め~終わりまでの一連の手順とその手順における方法を説明します。
2-1 一連の手順
★手順①が終わったら、次の手順②、それが終わったら、次の手順③というように進めば、
初級~上級の問題なら、手順③までで完成するはずです。
手順③までに完成しないときは、さらに手順④、手順⑤に進んで下さい。
超上級~名人級の問題でも、これで完成するはずです。
手順① 空きマスに入る候補になり得ない数字を探して削除する。
| 1.1 マス行内に入り得ない数字(既定の数字と同じ数字)消し 1.2 マス列内に入り得ない数字(既定の数字と同じ数字)消し 1.3 ブロック内に入り得ない数字(既定の数字と同じ数字)消し |
手順② 空きマスに入る候補がオンリーワンの数字を探して確定する。
| 2.1 マス行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.2 マス列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.3 ブロック内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.4 ブロック行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.5 ブロック列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し |
手順③ 上記2.1~2.5を繰り返す。
手順④ 空きマスに入る候補がオンリーツウの組数字を探して仮決めする。
| 4.1 マス行内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し 4.2 マス列内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し 4.3 ブロック内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し |
手順⑤ 上記2.1~2.5を繰り返す。
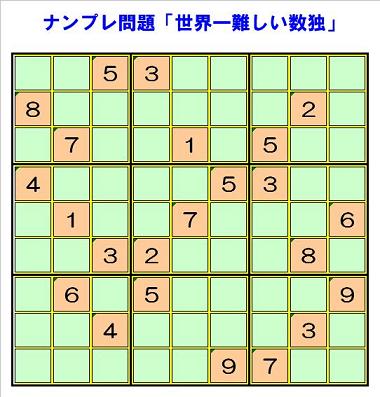
★なお、手順⑤を終えても、完成しないナンプレとしては、例えば、フィンランドの数学者
が作成したとされる 「世界一難しい数独」(下図参照)などがあります。
この種のナンプレは、普通の解き方では途中で行き詰まってしまうタイプで、行き詰ま
った後は、特定のマスの数字を仮決めし、仮決めしたことによって変化する局面でさら
に特定のマスの数字を仮決めし、その仮決め毎に矛盾が出るか否かを確認して行き、
矛盾が出たら戻ってくるという試行錯誤的な方法によって完成させるものです。
しかし、この種のナンプレにもスマートな解法が欲しいですね。 (今後の課題)
 |
2-2 方法の解説
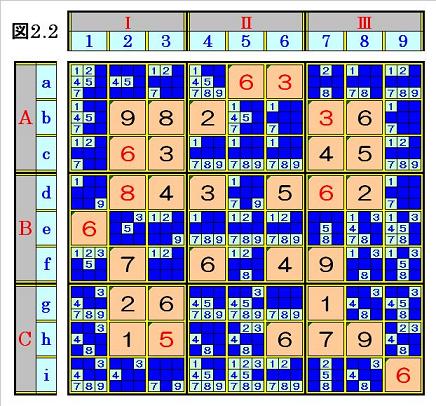
★先ず、ナンプレでどのマスにも数字が入っていないとき、マスに入る数字の候補は、
どのマスも1~9の全部です。 その最初の状態を下図のように表すことができます。
次に、いくつかのマスに1~9いずれかの数字が入った問題が作成されると、その数字が
入ったマス周辺の空きマスでは、入る数字の候補が自ずと制限されるようになります。
さらに、特定の空きマスに入る候補がオンリーワンになって数字が確定すると、
その確定したマス周辺の空きマスでは、入る数字の候補がさらに制限されていき、
次第に空きマスに数字が確定していくのです。
これを、下図のようなシート(以下、「必勝シート」 ということにします)を使って、
各空きマスに入り得ない数字を逐次塗りつぶしていくと、空きマスに入る候補が次第に
制限されて行く状況が見えるようになり、問題を解く手がかりを探し易くなります。
⇒本稿では、「必勝シート」 を使って、以下の方法を説明することにします。
 |
★手順①は、問題当初において、各空きマスに入る数字の候補が制限されている状況を
明らかにする手順です。
手順① 空きマスに入る候補になり得ない数字を探して削除する。
| 1.1 マス行内に入り得ない数字(既定の数字と同じ数字)消し 1.2 マス列内に入り得ない数字(既定の数字と同じ数字)消し 1.3 ブロック内に入り得ない数字(既定の数字と同じ数字)消し |
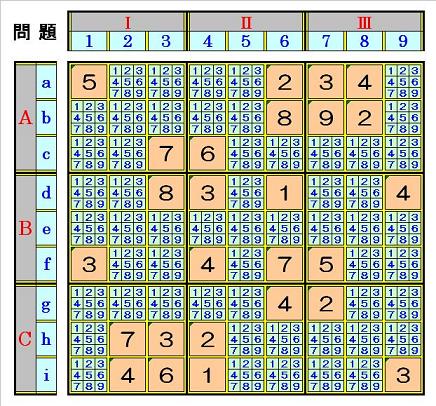 |
手順①1.1 マス行内に入り得ない数字(既定の数字と同じ数字)消し
上図 「問題」(上級問題)の例では、マス行aには5,2,3,4があるので、そのマス行aの
空きマスにある数字から候補になり得ない数字の5,2,3,4を塗りつぶします。
また、マス行bには8,9,2があるので、そのマス行bの空きマスにある数字から候補に
なり得ない数字の8,9,2を塗りつぶします。
マス行c~iも同様に、候補になり得ない数字を全部塗りつぶすと、次の図1.1の局面に
なり、次ステップへ行きます。
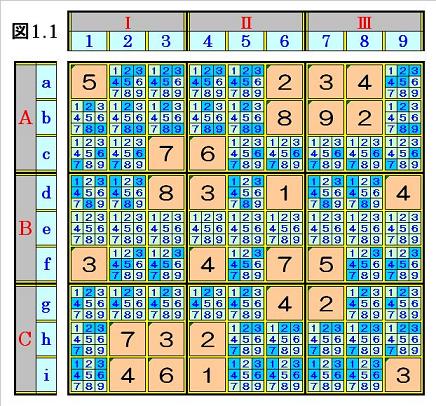 |
手順①1.2 マス列内に入り得ない数字(既定の数字と同じ数字)消し
図1.1において、マス列1には5,3があるので、そのマス列1の空きマスにある数字から
候補になり得ない数字の5,3を塗りつぶします。
前ステップまでに塗りつぶされているところはスルーします。 以下同様です。
(本稿では、塗りつぶしの色は、当初スカイブルーにし、次ステップで青に変更します)
また、マス列2には7,4があるので、そのマス列2の空きマスにある数字から候補になり
得ない数字の7,4を塗りつぶします。
マス列3~9も同様に、候補になり得ない数字を全部塗りつぶすと、次の図1.2の局面に
なり、次ステップへ行きます。
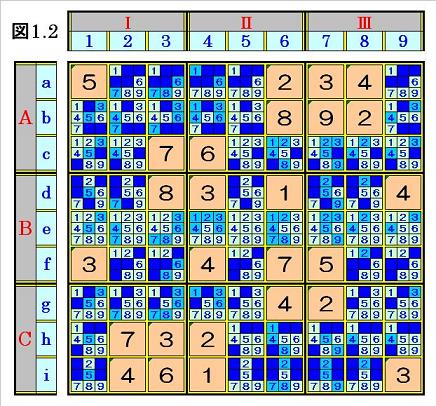 |
手順①1.3 ブロック内に入り得ない数字(既定の数字と同じ数字)消し
図1.2において、ブロックAⅠには5,7があるので、そのブロックAⅠの空きマスにある
数字から候補になり得ない数字の5,7を塗りつぶします。
また、ブロックAⅡには2,8,6があるので、そのブロックAⅡの空きマスにある数字から
候補になり得ない数字の2,8,6を塗りつぶします。
ブロックAⅢ~CⅢも同様に、候補になり得ない数字を全部塗りつぶすと、次の図1.3の
局面になり、次ステップへ行きます。
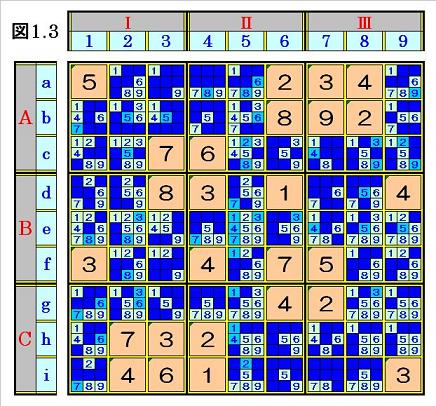 |
★手順②は、手順③,⑤でも繰り返すように、空きマスの数字を確定して行く手順です。
手順② 空きマスに入る候補がオンリーワンの数字を探して確定する。
| 2.1 マス行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.2 マス列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.3 ブロック内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.4 ブロック行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し 2.5 ブロック列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し |
手順②2.1 マス行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図1.3において、先ず、マス行a~iの順にマス行内の候補がオンリーワンになっていると
ころを探します。
マス行eではマスe8の3、マス行gではマスg5の3、マス行iではマスi1の2が、それぞれ、
そのマス行内で候補がオンリーワンになっており、確定できることがわかります。
そこで、先ずマスe8に3を入れて確定するとともに、そのマスe8が含まれるマス行eと
マス列8とブロックBⅢの空きマスにある数字から候補になり得ない数字の3を塗りつ
ぶすのですが、既に塗りつぶされています。
次に、マスg5に3を入れて確定するとともに、そのマスg5が含まれるマス行gとマス列5
とブロックCⅡの空きマスにある数字から3を塗りつぶします。
同様に、マスi1の2も数字を入れて確定するとともに、候補になり得ない数字の2を塗り
つぶすことにより、新たにマス行bではマスb2の3、マス行cではマスc2の2とマスc6の
3が、順次、そのマス行内で候補がオンリーワンになってきます。
そこで、数字の確定と、候補になり得ない数字の塗りつぶしを行うと、さらに、マス行dで
はマスd5の2とマスd2の5が、順次、確定できることになり、それらも同様に数字を入れ、
候補になり得ない数字を塗りつぶすと、次の図2.1の局面になり、他のマス行にオンリー
ワンがないことを確認した上で、次ステップへ行きます。
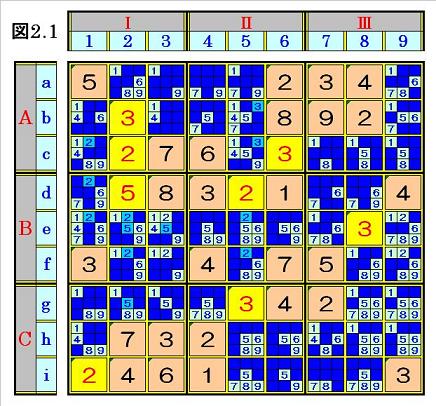 |
手順②2.2 マス列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図2.1において、先ず、マス列1~9の順にマス列内の候補がオンリーワンになっている
ところを探します。
マス列3ではマスg3の5、マス列7ではマスh7の4が、それぞれ、そのマス列内で候補が
オンリーワンになっているので、それぞれ確定するとともに、候補になり得ない数字を
塗りつぶすと、次の図2.2の局面になります。
他のマス列にオンリーワンがないことを確認して、次ステップへ行きます。
(本稿では、確定マスの色は、当初は黄で、次ステップで橙に変更しています)
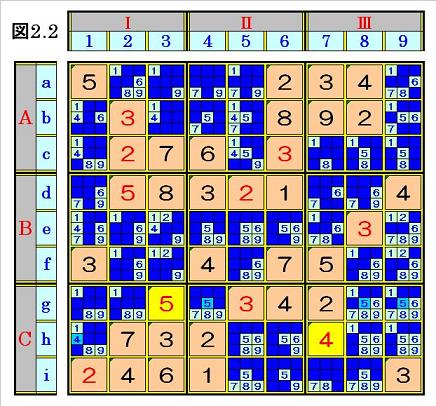 |
手順②2.3 ブロック内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図2.2において、ブロックAⅠ~CⅢの順にブロック内の候補がオンリーワンになって
いるところを探しますが、ありませんので、次ステップに行きます。
手順②2.4 ブロック行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
ブロック行のマスに入る1~9いずれの数字も、3つのブロック間で互いにマス行が異な
るマスに入ることになるため、図2.2において、ブロック行Aから、ブロック行内の数字
1~9の順にオンリーワンになっているところを探します。
オンリーワンのところはありませんが、ブロック行Cのマスh8とマスh9の6は候補に
なり得ないので、それを塗りつぶして次の図2.4の局面になり、次ステップへ行きます。
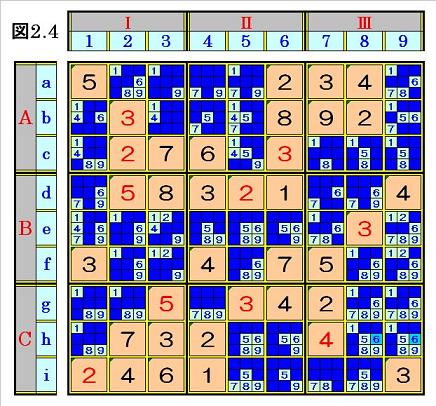 |
手順②2.5 ブロック列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
同様に、ブロック列のマスに入る1~9いずれの数字も、3つのブロック間で互いにマス列
が異なるマスに入ることになるため、図2.4において、ブロック列Ⅰから、ブロック列内
の数字1~9の順にオンリーワンになっているところを探します。
ブロック列Ⅲのマスe9の6,7、マスf9の6、マスg9の6,7は候補になり得ないので、それ
らを塗りつぶすと、マスg8の6はブロック列内でオンリーワンになって確定できます。
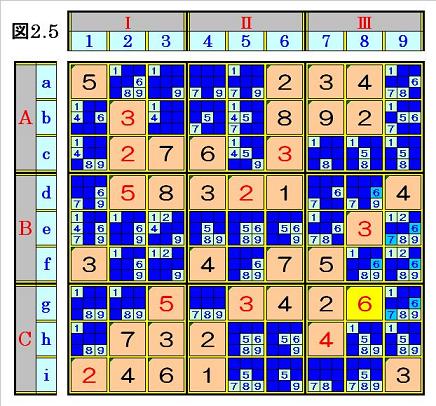
マスg8に6を入れるとともに、そのマスg8が含まれるマス行gとマス列8とブロックCⅢ
にある数字から候補になり得ない6を塗りつぶすと、次の図2.5の局面になり、次ステップ
へ行きます。
 |
手順③ 上記手順②の2.1~2.5を繰り返す。
手順③2.1 マス行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図2.5において、マス行a~iの順にマス行内の候補がオンリーワンになっているところを
探します。
マス行gでマスg4の7が、そのマス行内で候補がオンリーワンになっているので、マスg4
に7を入れるとともに、そのマスg4が含まれるマス行gとマス列4とブロックCⅡの空き
マスにある数字から候補になり得ない7を塗りつぶします。
そうすると、マス行aではマスa4の9、マス行bではマスb4の5が、それぞれオンリーワン
になってくるので、同様に、数字を入れて確定するとともに、候補になり得ない数字を塗り
つぶして行くと、新たにマス行aではマスa3の1、マス行dではマスd1の9とマスd7の6、
マス行eではマスe4の8が、順次、そのマス行内で候補がオンリーワンになってきます。
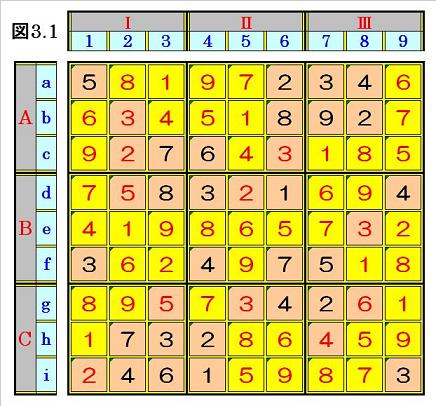
そこで、数字を入れて確定するとともに、候補になり得ない数字を塗りつぶして行くとい
う作業を繰り返すことにより、次々と空きマスの数字が確定して行き、結局、このステップ
で、図3.1のように完成してしまいます。
 |
★次の手順④は、空きマスに入る数字を確定するのではなく、新たにオンリーワンになる
ところをつくるために、空きマスに入る数字の候補にさらに制限を加える手順です。
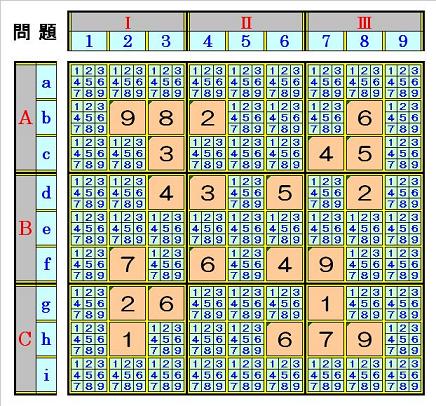
下図 「問題」(名人級)の例では、上記手順①~③を行っても、手順②の 「2.1マス行内
のオンリーワン数字探し・確定数字入れ+入り得ない数字消し」 のステップで一部の数
字が確定するものの、「2.2」 のステップ以降、全く変化がありません。
それで、次の図2.2の局面から、手順④を行うことにします。
手順④では、2個の数字の一方の数字が2箇所の一方のマスに入ると、他方の数字は他方
のマスに入るという関係にあるところを探し、そのマス2箇所をその2個の数字の組に
仮決めすることで、他の空きマスの候補を制限します。
 |
| 4.1 マス行内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し 4.2 マス列内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し 4.3 ブロック内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し |
 |
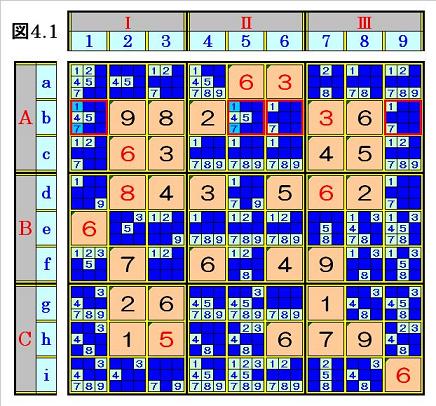
手順④4.1 マス行内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し
図2.2において、オンリーツウ(2個の数字の組が入るマスが、同じマス行の中で2箇所の
み)のところを探します。
オンリーツウとは、2個の数字の一方の数字が2箇所の一方のマスに入ると、他方の数字は
他方のマスに入るという関係にあることを意味します。
マス行bでは、マスb1の4,5とマスb5の4,5がオンリーツウになっているので、この2箇
所のマスb1とマスb5を4,5に仮決めし、そのマスにある他の数字(1,7)を塗りつぶし
組枠を入れます。
(本稿では、組枠の色は、当初は赤で、次ステップで濃赤に変更しています)
そうすると、マスb6中の1,7とマスb9の1,7がオンリーツウになってくるので、同様に
組枠を入れて、次の図4.1の局面になり、他のマス行にオンリーツウがないことを確認し
て、次ステップへ行きます。
 |
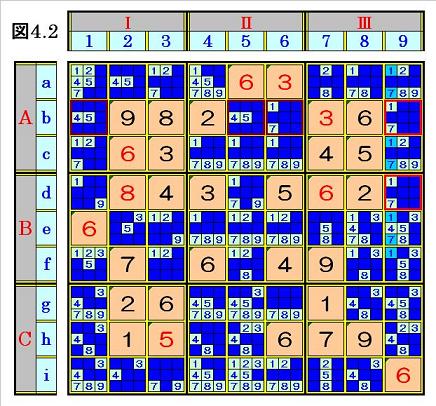
手順④4.2 マス列内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し
図4.1において、オンリーツウ(2個の数字の組が入るマスが、同じマス列の中で2箇所
のみ)のところを探します。
マス列9では、マスb9の1,7とマスd9の1,7がオンリーツウになっているので、1,7に
仮決めし組枠を入れます。
2箇所のマスb9とマスd9を1,7に仮決めすると、マス列9の他の空きマスには1,7が入
り得ないので、1,7を塗りつぶして、次の図4.2の局面になります。
他のマス列にオンリーツウがないことを確認して、次ステップへ行きます。
 |
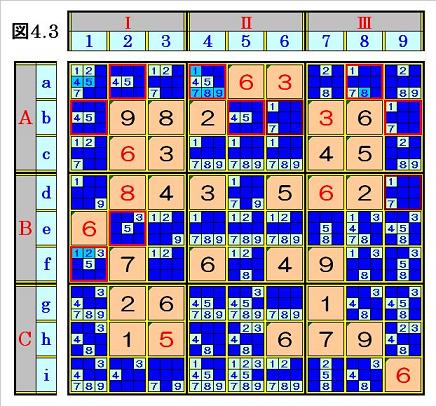
手順④4.3 ブロック内のオンリーツウ組数字探し・仮決め組枠入れ+入り得ない数字消し
図4.2において、オンリーツウ(2個の数字の組が入るマスが、同じブロックの中で2箇所
のみ)のところを探します。
ブロックAⅠでは、マスa2の4,5とマスd1の4,5がオンリーツウになっているので、4,5
に仮決めし組枠を入れます。
ブロックAⅡでは、マスa4の4,5とマスb5の4,5がオンリーツウになっているので、4,5
に仮決めし組枠を入れ、マスa4にある他の数字(1,7,8,9)を塗りつぶします。
ブロックAⅢでは、マスa8の1,7とマスb9の1,7がオンリーツウになっているので、1,7
に仮決めし組枠を入れ、マスa8の他の数字(8)を塗りつぶします。
ブロックBⅡでは、マスe2の3,5とマスf1の3,5がオンリーツウになっているので、3,5
に仮決めし組枠を入れ、マスf1の他の数字(1,2)を塗りつぶして、次の図4.3の局面に
なり、他のブロックにオンリーツウがないことを確認して、次ステップへ行きます。
 |
手順⑤ 上記手順②の2.1~2.5を繰り返す。
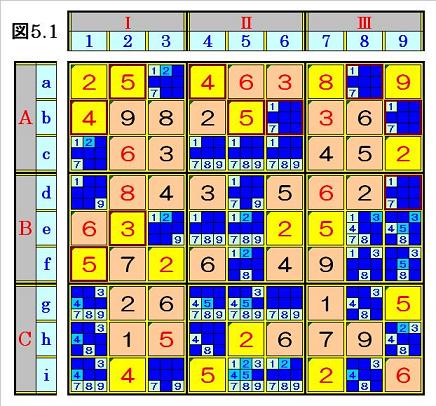
手順⑤2.1 マス行内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図4.3において、マス行a~iの順にマス行内の候補がオンリーワンになっているところ
を探します。
マス行aでマスa9の9が、オンリーワンなので、9を入れるとともに、そのマスa9が含ま
れるマス行aとマス列9とブロックAⅢの空きマスにある数字から9を塗りつぶします。
すると、マス行aでは、新たにマスa7の8が、オンリーワンになってくるので、同様に、
数字の確定と、候補になり得ない数字の塗りつぶしを行います。
そのように、順次、数字の確定と、候補になり得ない数字の塗りつぶしを行うことにより、
結局、次の図5.1の局面になり、他のマス行にオンリーワンがないことを確認した上で、
次ステップへ行きます。
 |
手順⑤2.2 マス列内のオンリーワン数字探し・確定数字入れ+入り得ない数字消し
図5.1において、先ず、マス列1~9の順にマス列内の候補がオンリーワンになっている
ところを探します。
マス列5では、マスg5の4が、オンリーワンになっているので、マスg5を確定するとと
もに、候補になり得ない数字を塗りつぶします。
すると、新たにマス列3では、マスh4の8が、マス列5では、マスi5の3が、マス列8では、
マスe8の4が、それぞれオンリーワンになってくるので、同様に、数字の確定と、候補に
なり得ない数字の塗りつぶしを行います。
そうすると、さらに、マス列1では、マスh1の3が、マス列6では、マスc6の8が、マス列8
では、マスa8の7が、マス列9では、マスh9の4が、それぞれオンリーワンになってくる
ので、同様に、数字の確定と、候補になり得ない数字の塗りつぶしを行います。
そのように、順次、数字の確定と、候補になり得ない数字の塗りつぶしを行う作業を繰り
返すことにより、次々と空きマスの数字が確定して行き、結局、このステップで、図5.2の
ように完成してしまうのです。
この手順⑤は、手順②の繰り返しに過ぎませんから、その前の手順④のオンリーツウ探し
が、難問の局面打開にとても有効であることがわかります。
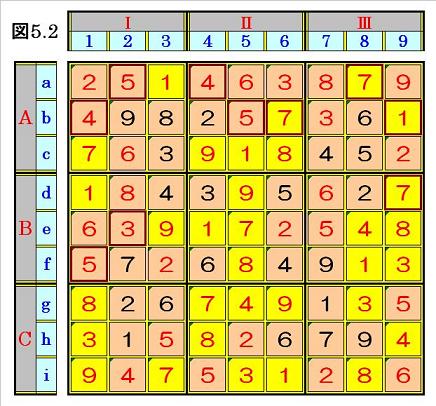 |
★なお、手順④では、2個の数字の一方の数字が2箇所の一方のマスに入ると、他方の数字は
他方のマスに入るという関係にあるところを探し、そのマス2箇所をその2個の数字の組
に仮決めすることで、他の空きマスの候補を制限するというオンリーツウに着目しました
が、これに似ているものとして、3個の数字の1個が3箇所のマスの1箇所に入ると、残りの
2個の数字は残りの2箇所のマスに入るという関係にあるところを探し、そのマス3箇所を
その3個の数字の組に仮決めすることで、他の空きマスの候補を制限するというオンリー
スリーに着目できるケースがあるかもしれません。

