1.はじめに
★リンク元の 「超必勝法」 では、空きマスに入る候補が次第に制限されて行く状況を見ることができるように、「必勝シート」 というものを使い、候補になり得ない数字を次々と
塗りつぶして行きました。
しかし、この 「超必勝法2」 では、「必勝シート」 を使わずに、
①始め~終わりまで一連の手順がある。
②初心者に理解できる基本の解法だけを使う。
③次にどの解法を用いればよいかがわかる。
ような方法であって、初心者でも名人級の難問を解くことができる方法を提案します。
1-1 マスの名称(リンク元、「超必勝法」 の 「1-1 マスの名称」 の再掲)
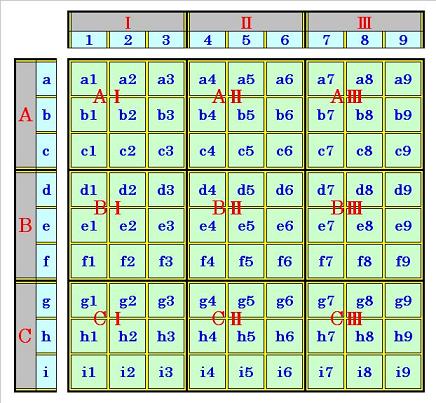
★説明上、先ず、9×9マスの標準的なナンプレについて、各部の名称を決めておきます。
①マス・マス行・マス列
全体に9×9個ある個々の枠を1つのマスとし、マスの横方向(⮕)のマス行をa~iの9個、
マスの縦方向(⬇)のマス列を1~9の9個として、各マスの位置を、左上のマスa1を基点
にして、それぞれ順に次のように表すことにします。
a1,a2・・・・a9、 b1,b2・・・・b9、 c1,c2・・・・c9、 d1,d2・・・・d9、 e1,e2・・・・e9、
f1,f2・・・・・f9、 g1,g2・・・・g9、 h1,h2・・・・h9、 i1,i2・・・・・i9
②ブロック・ブロック行・ブロック列
3×3個のマスが太線で囲まれた部分を1つのブロックとし、横方向(⮕)のブロック行を
A~Cの3行、縦方向(⬇)のブロック列をⅠ~Ⅲの3列として、各ブロックの位置を、左上
のブロックAⅠを基点にして、それぞれ順に次のように表すことにします。
AⅠ,AⅡ,AⅢ、BⅠ,BⅡ,BⅢ、CⅠ,CⅡ,CⅢ
 |
1-2 基本ルールの読み替え
★「必勝シート」 を使わないことから、リンク元、「超必勝法」 の 「1-2 基本ルール」 で、
実戦的に読み替えたものから、項目 「②a.b.c.」(候補になり得ない数字削除)を省略し、
次のように、項目 「①a.b.c.d.」 のみを使います。
| ①a.特定のマスに入る候補が1~9いずれかの数字1個のみのとき、そのマスはその数字 に確定できる。 b.特定のマスに入る候補が1~9いずれかの数字2個以上あっても、その内の数字1個 が入るマスが、その特定のマスがあるマス行かマス列かブロックの中で、そのマス 1箇所のみのとき、そのマスはその数字に確定できる。 c.ブロック行かブロック列のマスに入る数字は、3つのブロック間で互いにマス行か マス列が異なるマスに入ることになるため、その互いに異なるマス行かマス列で、 特定の数字が入り得るマスが1箇所のみのとき、そのマスはその数字に確定できる。 d.特定のマスに入る候補が1~9いずれかの数字2個以上であっても、その内の2個の 数字の組が入るマスが、同じマス行かマス列かブロックの中で2箇所のみのとき、 そのマス2箇所はその2個の数字の組に仮決めできる。 |
互いにマス行かマス列が異なるマスに入ることになる」 とは、次例のようなことです。
 |  |  |
 |  |  |
 |  |  |
★従って、これらを要約すると、次のようになります。
| ①a.b.c.オンリーワン数字確定 (候補がオンリーワンの数字を確定する) d. オンリーツウ組数字仮決め (候補がオンリーツウの組数字を仮決めする) |
★そこで、次の 「手順と方法」 では、上記項目 「①a.b.c.オンリーワン数字確定」 を行い、
これで完成しないときに、上記項目 「①d.オンリーツウ組数字仮決め」 を行うのは同様
ですが、上記項目①c.の 「ブロック行かブロック列のマスに入る数字は、3つのブロック
間で、互いにマス行かマス列が異なるマスに入ることになる」 点に着目し、
先ず、各ブロック行・ブロック列の数字配列を、数字1⇒9毎にチェックすることにより、
「オンリーワン数字確定」 できるところを増やすことから始めたいと思います。
令和 2 年 (西暦 2020 年) 2 月 22 日
令和 2 年 (西暦 2020 年) 3 月 20 日 改訂 ナンプレイヤー 球磨コレノリ

