ナンプレ超必勝法２ !!　　初心者コース

２．手順と方法

★リンク元の ｢超必勝法｣ で､空きマスに入る候補になり得ない数字を知るために使った
　｢必勝シート｣ を､この ｢超必勝法２｣ では使わずに､始め～終わりまでの一連の手順と
　その手順における方法を説明します｡
　　　　
2-1 一連の手順

★手順①が終わったら､次の手順②､それが終わったら､次の手順③というように進めば､
　初級～上級の問題なら､手順④までで完成するはずです｡
　手順④までに完成しないときは､さらに手順⑤､手順⑥に進んで下さい｡
　超上級～名人級の問題でも､これで完成するはずです｡

★手順①　各ブロック行･列の3ブロック間の数字配列を､数字1⇒9の順にチェックし､
　　　　　その数字が入るオンリーワンの空きマスがあれば､その数字に確定する｡

1.1  ブロック行毎に､3ブロック間で互いにマス行が異なるように数字入れ･確定   1.2  ブロック列毎に､3ブロック間で互いにマス列が異なるように数字入れ･確定

　手順②　上記手順①を繰り返す｡

　手順③　各空きマスがあるマス行･マス列･ブロック内の全数字1～9をチェックし､
　　　　　不足数字がオンリーワンの空きマスがあれば､その数字に確定する｡
　　　　　空きマスに数字が入って数字で埋まってくると､残った各空きマスのマス
　　　　　行･マス列･ブロックで､数字1～9が揃ってきます｡
　　　　　各空きマスがあるマス行･マス列･ブロックでは､数字のダブリは許されな
　　　　　いから､すべての数字1～9をチェックすることにより､不足数字がわかり､
　　　　　その不足数字がオンリーワンであれば､その数字に確定できます｡

3.1  マス行毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定   3.2  マス列毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定

　手順④　上記手順①～③を繰り返す｡

　手順⑤　空きマスに入る候補がオンリーツウの組数字を探して仮決めする｡

5.1  マス行内のオンリーツウ組数字探し･仮決め   5.2  マス列内のオンリーツウ組数字探し･仮決め   5.3  ブロック内のオンリーツウ組数字探し･仮決め

　手順⑥　上記手順①～⑤を繰り返す｡
　　　　
2-2 方法の解説

【上級問題に適用した例】
★手順①　各ブロック行･列の3ブロック間の数字配列を､数字1⇒9の順にチェックし､
　　　　　その数字が入るオンリーワンの空きマスがあれば､その数字に確定する｡

1.1  ブロック行の3ブロック間で互いにマス行が異なるように数字入れ･確定   1.2  ブロック列の3ブロック間で互いにマス列が異なるように数字入れ･確定
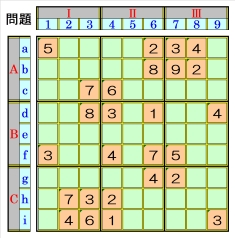	左記上級問題の例を図1～25で説明します｡ 上記手順①1.1～1.2を併行して､数字1⇒9 の順に行います｡
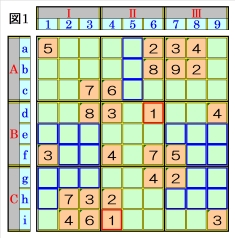	上図で､数字1に着目して手順①を行います｡ 数字1は､マスd6とマスi4にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字1が入る空きマスを､図1の青枠で示しま すが､どれも確定できません｡
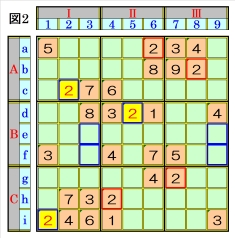	上図で､数字2に着目して手順①を行います｡ 数字2は､マスa6,マスb8,マスg7,マスh4に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字2が入る空きマスを､図 2の青枠で示します｡ ブロック行Cで､マスg7,マスh4の数字2か ら､マスi1は､数字2に確定でき､ブロック行A で､マスa6,マスb8の数字2から､マスc2も､ 数字2に確定できます｡ また､ブロック列Ⅰで､マスc2,マスi1の数字2 から､マスe3かマスf3に数字2が入ることに なると共に､ブロック列Ⅲで､マスb8,マスg7 の数字2から､マスe9かマスf9に数字2が入る ことになるため､ブロック行Bで､マスd5は､ 数字2に確定できます｡
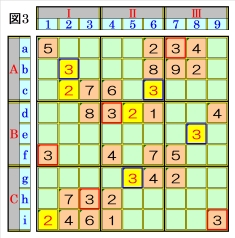	上図で､数字3に着目して手順①を行います｡ 数字3は､マスa7,マスd4,マスf1,マスh3,マ スi9にあるので､その各マスがある各ブロック 行･ブロック列の3ブロック間で互いにマス行･ マス列が異なるように数字3が入る空きマス を､図3の青枠で示します｡ ブロック行Bで､マスd4,マスf1の数字3から､ マスe8は､数字3に確定でき､ブロック行Cで､ マスh3,マスi9の数字3から､マスg5も､数字 3に確定できます｡ また､ブロック列Ⅰで､マスf1,マスh3の数字 3から､マスb2は､数字3に確定でき､ブロック 列Ⅱで､マスd4,マスg5の数字3から､マスc6 も､数字3に確定できます｡
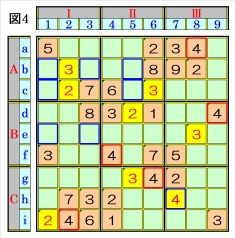	上図で､数字4に着目して手順①を行います｡ 数字4は､マスa8,マスd9,マスf4,マスg6,マ スi2にあるので､その各マスがある各ブロック 行･ブロック列の3ブロック間で互いにマス行･ マス列が異なるように数字4が入る空きマス を､図4の青枠で示します｡ ブロック行Cで､マスg6,マスi2の数字4から､ マスh7は､数字4に確定できます｡
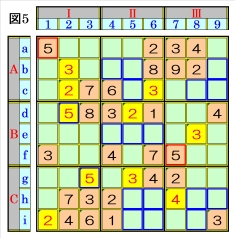	上図で､数字5に着目して手順①を行います｡ 数字5は､マスa1,マスf7にあるので､その各マ スがある各ブロック行･ブロック列の3ブロッ ク間で互いにマス行･マス列が異なるように 数字5が入る空きマスを､図5の青枠で示しま す｡ ブロック行Bで､マスf7の数字5から､マスe4 かマスe5かマスe6に数字5が入ることになる ため､マスd2は､数字5に確定でき､ブロック列 Ⅰで､マスa1,マスd2の数字5から､マスg3 も､数字5に確定できます｡
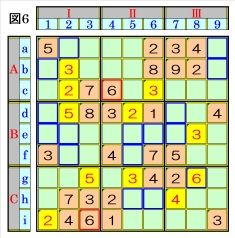	上図で､数字6に着目して手順①を行います｡ 数字6は､マスc4,マスi3にあるので､その各マ スがある各ブロック行･ブロック列の3ブロッ ク間で互いにマス行･マス列が異なるように数 字6が入る空きマスを､図6の青枠で示します｡ ブロック行Aで､マスc4の数字6から､マスa9 かマスb9に数字6が入ることになると共に､ ブロック行Cで､マスi3の数字6から､マスh5 かマスh6に数字6が入ることになるため､マス g8は､数字6に確定できます｡
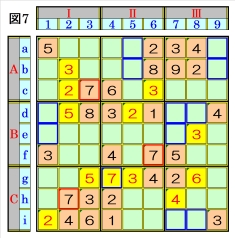	上図で､数字7に着目して手順①を行います｡ 数字7は､マスc3,マスf6,マスh2にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字7が入る空きマスを､図7の青枠で 示します｡ ブロック行Aで､マスc3の数字7から､マスa9 かマスb9に数字7が入ることになるので､ブロ ック列Ⅲで､数字7は､マスi7かマスi8に入る ことになるため､ブロック行Cで､マスh2の数 字7から､マスg4は､数字7に確定できます｡
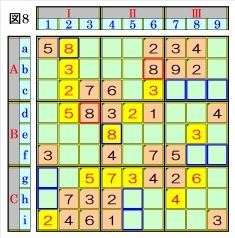	上図で､数字8に着目して手順①を行います｡ 数字8は､マスb6,マスd3にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字8が入る空きマスを､図8の青枠で示しま す｡ ブロック行Aで､マスa9,マスb9には､数字6, 7が入ることになるため､数字8は､マスc7か マスc8かマスc9に入ることになり､マスb6の 数字8から､マスa2は､数字8に確定し､ブロッ ク列Ⅱで､マスb6の数字8から､マスh5かマ スi5に数字8が入ることになるため､マスe4 は､数字8に確定できます｡
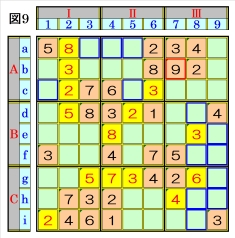	上図で､数字9に着目して手順①を行います｡ 数字9は､マスb7にあるので､そのマスがある ブロック行･ブロック列の3ブロック間で互い にマス行･マス列が異なるように数字9が入る 空きマスを､図9の青枠で示しますが､どれも 確定できません｡

★手順②　上記手順①を繰り返す｡

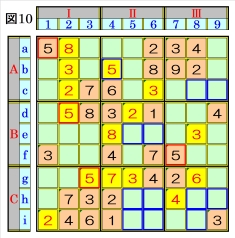	上記図1～9で､上記手順①を数字1⇒9の順に 行いましたが､手順①による数字入れができな くなるまで､これを繰り返します｡ 上図で､数字5に着目して手順①を行います｡ 数字5は､マスa1,マスd2,マスf7,マスg3に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字5が入る空きマスを､図 10の青枠で示します｡ ブロック行Bで､マスd2,マスf7の数字5から､ マスe5かマスe6に数字5が入ることになると 共に､ブロック行Cで､マスg3の数字5から､マ スh5かマスh6かマスi5かマスi6に数字5が 入ることになるため､ブロック列Ⅱで､マスb4 は､数字5に確定できます｡
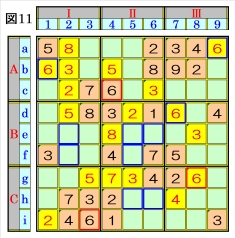	上図で､数字6に着目して手順①を行います｡ 数字6は､マスc4,マスg8,マスi3にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字6が入る空きマスを､図11の青枠で 示します｡ ブロック行Aで､マスc4の数字6から､数字6が マスb1,マスa9に入ることが確定でき､ブロッ ク列Ⅰで､マスb1,マスi3の数字6から､数字6 がマスe2かマスf2に入ることになると共に､ ブロック行Bで､数字6がマスe5かマスe6か マスf5に入ることになるため､マスd7は､数字 6に確定できます｡
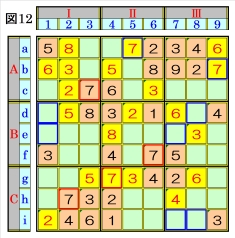	上図で､数字7に着目して手順①を行います｡ 数字7は､マスc3,マスf6,マスg4,マスh2に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字7が入る空きマスを､図 12の青枠で示します｡ ブロック行Aで､マスc3の数字7から､マスa5, マスb9は､数字7に確定できます｡

★手順③　各空きマスがあるマス行･マス列･ブロック内の全数字1～9をチェックし､
　　　　　不足数字がオンリーワンの空きマスがあれば､その数字に確定する｡
　　　　　空きマスに数字が入って数字で埋まってくると､残った各空きマスがある
　　　　　マス行･マス列･ブロックで､数字1～9が揃ってきます｡
　　　　　各空きマスがあるマス行･マス列･ブロックでは､数字のダブリは許されな
　　　　　いから､すべての数字1～9をチェックすることにより､不足数字がわかり､
　　　　　その不足数字がオンリーワンであれば､その数字に確定できます｡

3.1  マス行毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定   3.2  マス列毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定
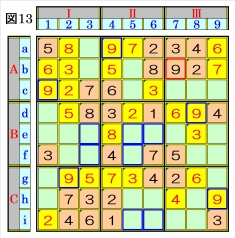	上記手順③3.1～3.2を併行して､数字1⇒9 の順に行います｡ 図13で､マスa4は､マス列4のオンリーワンの 不足数字で､数字9に確定できるので､数字9に 着目して手順①を行います｡ 数字9は､マスa4,マスb7にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字9が入る空きマスを､図13の青枠で示しま す｡ ブロック行Aで､マスa4,マスb7の数字9か ら､マスc1の数字9が確定でき､ブロック列Ⅰ で､マスc1の数字9から､マスg2の数字9が確 定でき､ブロック行Bで､数字9は､マスe3かマ スf3とマスe5かマスe6かマスf5に入ること になるため､マスd8の数字9が確定でき､ブロ ック列Ⅲで､マスb7,マスd8の数字9から､マ スh9の数字9が確定します｡
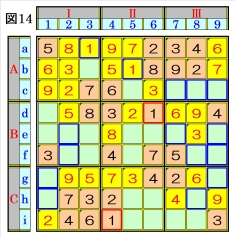	図14で､マスa3は､マス行aのオンリーワンの 不足数字で､数字1に確定できるので､数字1に 着目して手順①を行います｡ 数字1は､マスa3,マスd6,マスi4にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字1が入る空きマスを､図14の青枠で 示します｡ ブロック行Aで､数字1は､マスc7かマスc8か マスc9に入ることになるため､マスa3の数字 1から､マスb5の数字1が確定します｡
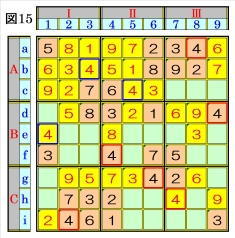	図15で､マスb3,マスc5は､それぞれブロック AⅠ,ブロックAⅡのオンリーワンの不足数字 で､それぞれ数字4に確定できるので､数字4に 着目して手順①を行います｡ 数字4は､マスa8,マスb3,マスc5,マスd9,マ スf4,マスg6,マスh7,マスi2にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字4が入る空きマスを､図15の青枠で示 します｡ ブロック列Ⅰで､マスb3,マスi2の数字4から､ マスe1は､数字4に確定できます｡
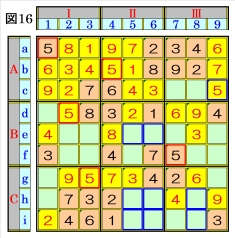	上図で､数字5に着目して手順①を行います｡ 数字5は､マスa1,マスb4,マスd2,マスf7,マ スg3にあるので､その各マスがある各ブロッ ク行･ブロック列の3ブロック間で互いにマス 行･マス列が異なるように数字5が入る空きマ スを､図16の青枠で示します｡ ブロック列Ⅲで､マスf7の数字5から､数字5 は､マスh8かマスi8に入ることになるため､マ スc9は､数字5に確定できます｡
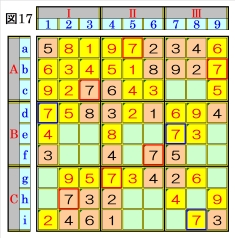	図17で､マスd1は､マス行dのオンリーワンの 不足数字で､数字7に確定できるので､数字7に 着目して手順①を行います｡ 数字7は､マスa5,マスb9,マスc3,マスd1,マ スf6,マスg4,マスh2にあるので､その各マス がある各ブロック行･ブロック列の3ブロック 間で互いにマス行･マス列が異なるように数字 7が入る空きマスを､図17の青枠で示します｡ ブロック行Bで､マスd1,マスf6の数字7から､ マスe7の数字7が確定し､ブロック列Ⅲで､マ スb9,マスe7の数字7から､マスi8の数字7が 確定します｡
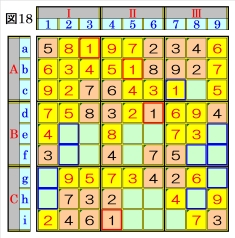	上図で､数字1に着目して手順①を行います｡ 数字1は､マスa3,マスb5,マスd6,マスi4に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字1が入る空きマスを､図 18の青枠で示します｡ 数字1は､ブロック列Ⅰでは､マスg1かマスh1 に入ることになるため､ブロック行Cでは､マス g9かマスh8に入ることになる共に､ブロック 列Ⅲでは､マスe9かマスf8かマスf9に入るこ とになるため､マスc7の数字1が確定します｡
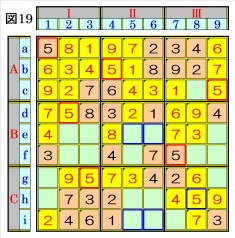	上図で､数字5に着目して手順①を行います｡ 数字5は､マスa1,マスb4,マスc9,マスd2,マ スf7,マスg3にあるので､その各マスがある各 ブロック間で互いにマス行･マス列が異なるよ うに数字5が入る空きマスを､図19の青枠で示 します｡ ブロック列Ⅲで､マスc9,マスf7の数字5から､ マスh8は､数字5に確定できます｡
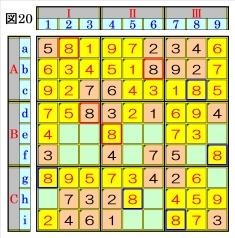	図20で､マスc8,マスi7は､それぞれマス行c, マス列7のオンリーワンの不足数字で､それぞ れ数字8に確定できるので､数字8に着目して 手順①を行います｡ 数字8は､マスa2,マスb6,マスc8,マスd3,マ スe4にあるので､その各マスがある各ブロッ ク行･ブロック列の3ブロック間で互いにマス 行･マス列が異なるように数字8が入る空きマ スを､図20の青枠で示します｡ ブロック列Ⅲで､マスc8,マスi7の数字8から､ マスf9の数字8が確定し､ブロック行Cで､マス i7の数字8から､マスg1,マスh5は､数字8に 確定できます｡
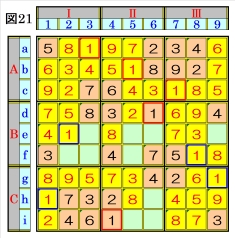	図21で､マスh1,マスf8,マスg9は､それぞれ マス列1,マス列8,マス行gのオンリーワンの 不足数字で､それぞれ数字1に確定できるので､ 数字1に着目して手順①を行います｡ 数字1は､マスa3,マスb5,マスc7,マスd6,マ スf8,マスg9,マスh1,マスi4にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字1が入る空きマスを､図21の青枠で示 します｡ ブロック行Bで､マスd6,マスf8の数字1から､ マスe2は､数字1に確定できます｡
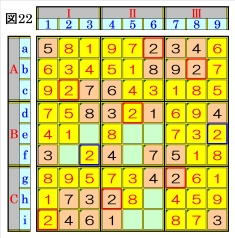	図22で､マスe9は､マス列9のオンリーワンの 不足数字で､数字2に確定できるので､数字2に 着目して手順①を行います｡ 数字2は､マスa6,マスb8,マスc2,マスd5,マ スe9,マスg7,マスh4,マスi1にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字2が入る空きマスを､図22の青枠で示 します｡ ブロック行Bで､マスd5,マスe9の数字2か ら､マスf3は､数字2に確定できます｡
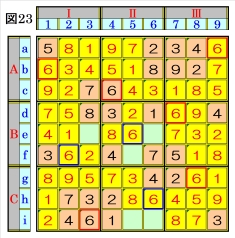	図23で､マスf2,マスh6は､それぞれマス列2, マス行hのオンリーワンの不足数字で､それぞ れ数字6に確定できるので､数字6に着目して 手順①を行います｡ 数字6は､マスa9,マスb1,マスc4,マスd7,マ スf2,マスg8,マスh6,マスi3にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字6が入る空きマスを､図23の青枠で示 します｡ ブロック行Bで､マスd7,マスf2の数字6から､ マスe5は､数字6に確定できます｡
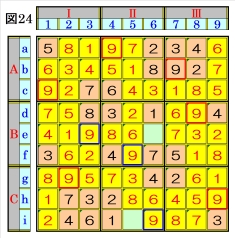	図24で､マスe3,マスf5は､それぞれマス列3, マス行fのオンリーワンの不足数字で､それぞ れ数字9に確定できるので､数字9に着目して 手順①を行います｡ 数字9は､マスa4,マスb7,マスc1,マスd8,マ スe3,マスf5,マスg2,マスh9にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字9が入る空きマスを､図24の青枠で示 します｡ ブロック列Ⅱで､マスa4,マスf5の数字9から､ マスi6は､数字9に確定できます｡
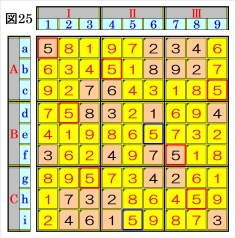	図25で､マスe6,マスi5は､それぞれマス行e, マス行iのオンリーワンの不足数字で､それぞ れ数字5に確定できます｡ これで､この上級問題の例のすべての数字が確 定しました｡

【名人級問題に適用した例】

★手順①　各ブロック行･列の3ブロック間の数字配列を､数字1⇒9の順にチェックし､
　　　　　その数字が入るオンリーワンの空きマスがあれば､その数字に確定する｡

1.1  ブロック行の3ブロック間で互いにマス行が異なるように数字入れ･確定   1.2  ブロック列の3ブロック間で互いにマス列が異なるように数字入れ･確定
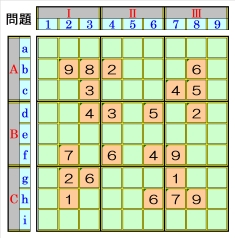	左記名人級問題の例を図1～35で説明します｡ 上記手順①1.1～1.2を併行して､数字1⇒9 の順に行います｡
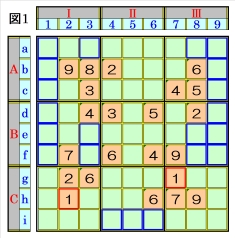	上図で､数字1に着目して手順①を行います｡ 数字1は､マスg7,マスh2にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字1が入る空きマスを､図1の青枠で示しま すが､どれも確定できません｡
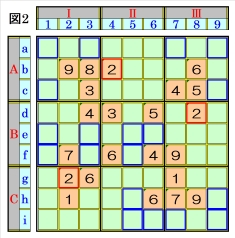	上図で､数字2に着目して手順①を行います｡ 数字2は､マスb4,マスd8,マスg2にあるの で､その各マスがある各ブロック行･ブロック 列の3ブロック間で互いにマス行･マス列が異 なるように数字2が入る空きマスを､図2の青 枠で示しますが､どれも確定できません｡
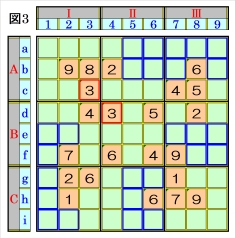	上図で､数字3に着目して手順①を行います｡ 数字3は､マスc3,マスd4にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字3が入る空きマスを､図3の青枠で示しま すが､どれも確定できません｡
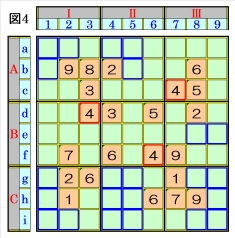	上図で､数字4に着目して手順①を行います｡ 数字4は､マスc7,マスd3,マスf6にあるので､ その各マスがある各ブロック行･ブロック列の の3ブロック間で互いにマス行･マス列が異な るように数字4が入る空きマスを､図4の青枠 で示しますが､どれも確定できません｡
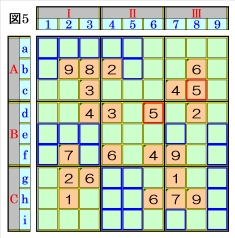	上図で､数字5に着目して手順①を行います｡ 数字5は､マスc8,マスd6にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字5が入る空きマスを､図5の青枠で示しま すが､どれも確定できません｡
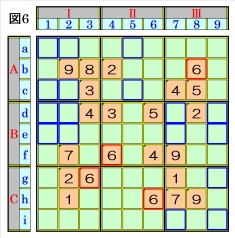	上図で､数字6に着目して手順①を行います｡ 数字6は､マスb8,マスf4,マスg3,マスh6に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字6が入る空きマスを､図 6の青枠で示しますが､どれも確定しません｡
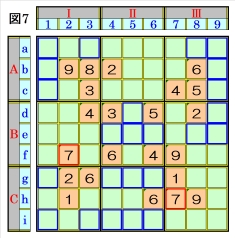	上図で､数字7に着目して手順①を行います｡ 数字7は､マスf2,マスh7にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字7が入る空きマスを､図7の青枠で示しま すが､どれも確定できません｡
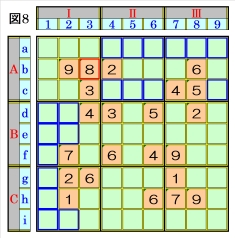	上図で､数字8に着目して手順①を行います｡ 数字8は､マスb3にあるので､そのマスがある ブロック行･ブロック列の3ブロック間で互い にマス行･マス列が異なるように数字8が入る 空きマスを､図8の青枠で示しますが､どれも 確定できません｡
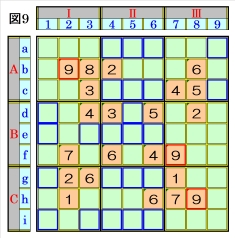	上図で､数字9に着目して手順①を行います｡ 数字9は､マスb2,マスf7,マスh8にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字9が入る空きマスを､図9の青枠で 示しますが､どれも確定できません｡

★手順③　各空きマスがあるマス行･マス列･ブロック内の全数字1～9をチェックし､
　　　　　不足数字がオンリーワンの空きマスがあれば､その数字に確定する｡
　　　　　空きマスに数字が入って数字で埋まってくると､残った各空きマスがある
　　　　　マス行･マス列･ブロックで､数字1～9が揃ってきます｡
　　　　　それで､数字が4個以上に多いマス行･マス列･ブロックをチェックします｡
　　　　　各空きマスがあるマス行･マス列･ブロックでは､数字のダブリは許されな
　　　　　いため､すべての数字1～9をチェックすることによって､不足数字がわか
　　　　　り､その不足数字がオンリーワンであれば､その数字に確定できます｡

3.1  マス行毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定   3.2  マス列毎に､各空きマスがあるマス行･マス列･ブロックの不足数字探し･確定
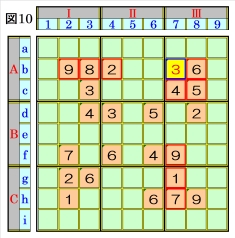	上記手順③3.1～3.2を併行して､数字1⇒9 の順に行います｡ 図10で､マスb7があるマス行b･マス列7･ブ ロックAⅢで､数字1～9をチェックすると､マ スb7は､オンリーワンの不足数字で､数字3に 確定できます｡
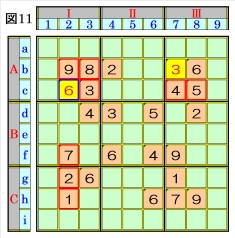	図11で､マスc2があるマス行c･マス列2･ブ ロックAⅠで､数字1～9をチェックすると､マ スc2は､オンリーワンの不足数字で､数字6に 確定できます｡
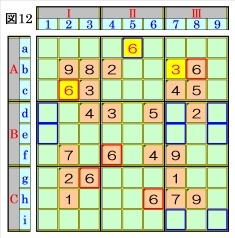	上図で､数字6に着目して手順①を行います｡ 数字6は､マスb8,マスc2,マスf4,マスg3,マ スh6にあるので､その各マスがある各ブロッ ク行･ブロック列の3ブロック間で互いにマス 行･マス列が異なるように数字6が入る空きマ スを､図12の青枠で示します｡ ブロック列Ⅱで､マスf4,マスh6の数字6か ら､マスa5は､数字6に確定できます｡
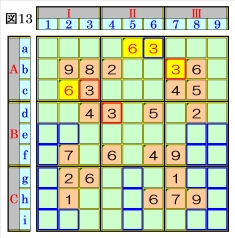	上図で､数字3に着目して手順①を行います｡ 数字3は､マスb7,マスc3,マスd4にあるの で､その各マスがある各ブロック行･ブロック 列の3ブロック間で互いにマス行･マス列が異 なるように数字3が入る空きマスを､図13の青 枠で示します｡ ブロック行Aで､マスb7,マスc3の数字3から､ マスa6は､数字3に確定できます｡
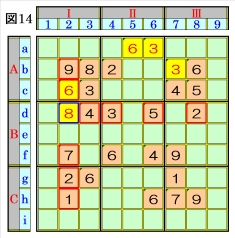	図14で､マスd2があるマス行d･マス列2･ブ ロックBⅠで､数字1～9をチェックすると､マ スd2は､オンリーワンの不足数字で､数字8に 確定できます｡
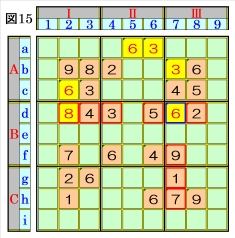	図15で､マスd7があるマス行d･マス列7･ブ ロックBⅢで､数字1～9をチェックすると､マ スd7は､オンリーワンの不足数字で､数字6に 確定できます｡
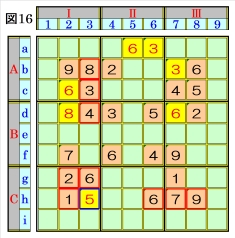	図16で､マスh3があるマス行h･マス列3･ブ ロックCⅠで､数字1～9をチェックすると､マ スh3は､オンリーワンの不足数字で､数字5に 確定できます｡
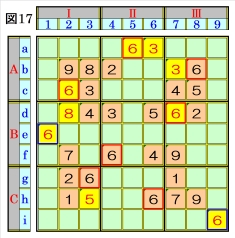	上図で､数字6に着目して手順①を行います｡ 数字6は､マスa5,マスb8,マスc2,マスd7,マ スf4,マスg3,マスh6にあるので､その各マス がある各ブロック行･ブロック列の3ブロック 間で互いにマス行･マス列が異なるように数字 6が入る空きマスを､図17の青枠で示します｡ ブロック行Bで､マスd7,マスf4の数字6から､ マスe1は､数字6に確定でき､ブロック行Cで､ マスg3,マスh6の数字6から､マスi9も､数字 6に確定できます｡

★手順⑤　空きマスに入る候補がオンリーツウの組数字を探して仮決めする｡
　　　　　上記手順③で､空きマスがオンリーワンの不足数字に確定してくると､次に､
　　　　　オンリーツウの不足数字を探して､一対の組数字があれば､仮決めにします｡
　　　　　オンリーツウの組数字とは､一対の数字の一方が2箇所の一方のマスに入る
　　　　　と､他方の数字が他方のマスに入るという関係にある組数字を意味します｡

5.1  マス行内のオンリーツウ組数字探し･仮決め   5.2  マス列内のオンリーツウ組数字探し･仮決め   5.3  ブロック内のオンリーツウ組数字探し･仮決め
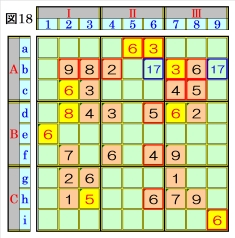	上記手順⑤5.1～5.3を併行して､数字1⇒9 の順に行います｡ 図18で､マスb6があるマス行b･マス列6･ブ ロックAⅡで､数字1～9をチェックすると､マ スb6は､数字1,7が不足するオンリーツウの 組数字1,7に仮決めでき､また､マスb9がある マス行b･マス列9･ブロックAⅢで､数字1～9 をチェックすると､マスb9も､数字1,7が不足 するオンリーツウの組数字1,7に仮決めでき ます｡
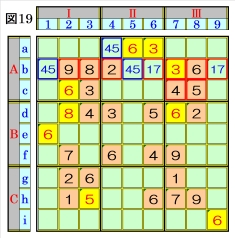	図19で､マスb1,マスb5は､それぞれマス行b で数字4,5が不足するオンリーツウの組数字4 ,5に仮決めできるので､組数字4,5に着目して 手続①を行います｡ ブロック行Aで､マスb1のオンリーツウの組数 字4,5とマスc7の数字4とマスc8の数字5と から､ブロックAⅡのマスa4は､マスb5とのオ ンリーツウの組数字4,5に仮決めできます｡
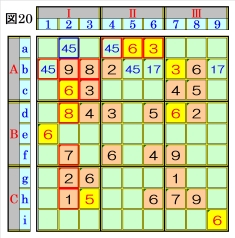	図20で､マスa2があるマス行a･マス列2･ブ ロックAⅠで､数字1～9をチェックすると､マ スa2は､数字4,5が不足し､これは､マス行a のマスa4とのオンリーツウの組数字であると 共に､ブロックAⅠのマスb1とのオンリーツウ の組数字でもあって､組数字4,5に仮決めでき ます｡
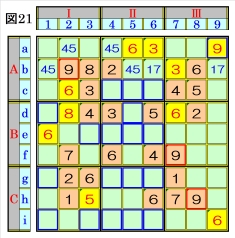	上図で､数字9に着目して手続①を行います｡ 数字9は､マスb2,マスf7,マスh8にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字9が入る空きマスを､図21の青枠で 示します｡ ブロック行Aで､マスb2とマスc4かマスc5か マスc6に入る数字9から､マスa9は､数字9に 確定できます｡
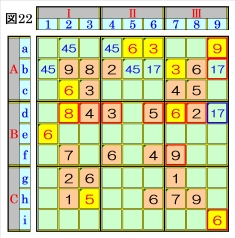	図22で､マスd9があるマス行d･マス列9･ブ ロックBⅢで､数字1～9をチェックすると､マ スd9は､数字1,7が不足し､これは､マス列9の マスb9とのオンリーツウの組数字であり､組 数字1,7に仮決めできます｡
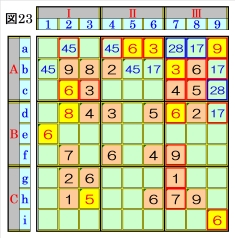	図23で､マスa7があるマス行a･マス列7･ブ ロックAⅢで､数字1～9をチェックすると､マ スa7は､数字2,8が不足し､また､マスc9があ るマス行c･マス列9･ブロックAⅢで､数字1～ 9をチェックすると､マスc9は､数字2,8が不 足するので､マスa7,マスc9は､ブロックAⅢ のオンリーツウの組数字2,8に仮決めできま す｡ 加えて､マスa8は､ブロックAⅢのマスb9との オンリーツウの組数字1,7に仮決めできます｡
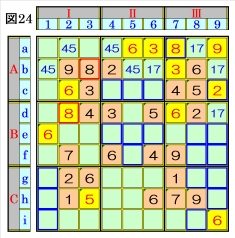	上図で､数字8に着目して手順①を行います｡ 数字8は､マスb3,マスd2にあるので､その各 マスがある各ブロック行･ブロック列の3ブロ ック間で互いにマス行･マス列が異なるように 数字8が入る空きマスを､図24の青枠で示しま す｡ ブロック行Aで､マスb3とマスc4かマスc5か マスc6に入ることになる数字8から､マスa7 の組数字2,8は､数字8に確定し､併せて､マス c9の組数字2,8は､数字2に確定します｡
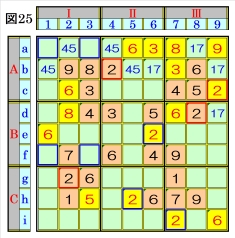	上図で､数字2に着目して手順①を行います｡ 数字2は､マスb4,マスc9,マスd8,マスg2に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字2が入る空きマスを､図 25の青枠で示します｡ ブロック列Ⅲで､マスc9,マスd8の数字2か ら､マスi7は､数字2に確定でき､ブロック行C で､マスg2,マスi7の数字2から､マスh5は､数 字2に確定でき､ブロック列Ⅱで､マスb4,マス h5の数字2から､マスe6も､数字2に確定でき ます｡
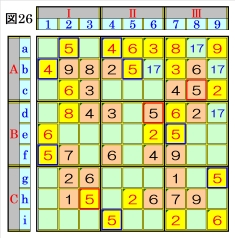	図26で､マスe7は､マス列7のオンリーワンの 不足数字で､数字5に確定できるので､数字5に 着目して手順①を行います｡ 数字5は､マスa2かマスa4,マスb1かマスb5, マスc8,マスd6,マスh3にあるので､その各マ スがある各ブロック行･ブロック列の3ブロッ ク間で互いにマス行･マス列が異なるように数 字5が入る空きマスを､図26の青枠で示しま す｡ ブロック行Bで､マスd6,マスe7の数字5か ら､マスf1は､数字5に確定し､ブロック列Ⅲ で､マスc8,マスe7の数字5から､マスg9は､ 数字5に確定します｡ ブロック列Ⅰで､マスf1,マスh3の数字5か ら､マスa2の組数字4,5は､数字5に確定し､ブ ロック行Aで､マスa2,マスc8の数字5から､ マスb5の組数字4,5は､数字5に確定し､ブロ ック列Ⅱで､マスb5,マスd6の数字5から､マ スi4も､数字5に確定します｡ 併せて､組数字4,5のマスa2,マスb5がそれぞ れ数字5に確定したため､マスa4,マスb1の組 数字4,5は､それぞれ数字4に確定します｡
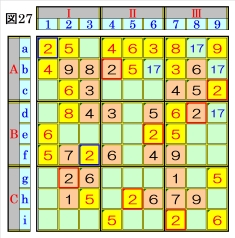	上図で､数字2に着目して手順①を行います｡ 数字2は､マスb4,マスc9,マスd8,マスe6,マ スg2,マスh5,マスi7にあるので､その各マス がある各ブロック行･ブロック列の3ブロック 間で互いにマス行･マス列が異なるように数字 2が入る空きマスを､図27の青枠で示します｡ ブロック行Bで､マスd8,マスe6の数字2か ら､マスf3は､数字2に確定でき､ブロック列Ⅰ で､マスf3,マスg2の数字2から､マスa1も､ 数字2に確定できます｡
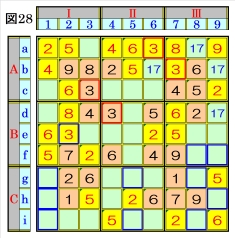	上図で､数字3に着目して手順①を行います｡ 数字3は､マスa6,マスb7,マスc3,マスd4に あるので､その各マスがある各ブロック行･ブ ロック列の3ブロック間で互いにマス行･マス 列が異なるように数字3が入る空きマスを､図 28の青枠で示します｡ ブロック列Ⅰで､マスc3の数字3から､マスe2 は､数字3に確定できます｡
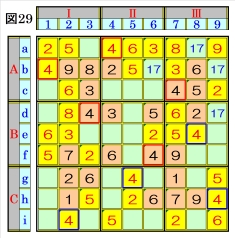	図29で､マスi2は､マス列2のオンリーワンの 不足数字で､数字4に確定できるので､数字4に 着目して手順①を行います｡ 数字4は､マスa4,マスb1,マスc7,マスd3,マ スf6,マスi2にあるので､その各マスがある各 ブロック行･ブロック列の3ブロック間で互い にマス行･マス列が異なるように数字4が入る 空きマスを､図29の青枠で示します｡ ブロック行Cで､マスi2の数字4から､マスg5, マスh9は､数字4に確定でき､ブロック列Ⅲで､ マスc7,マスh9の数字4から､マスe8も､数字 4に確定できます｡
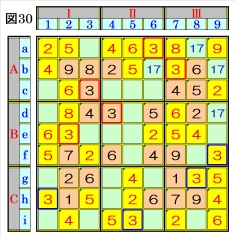	上図で､数字3に着目して手順①を行います｡ 数字3は､マスa6,マスb7,マスc3,マスd4,マ スe2にあるので､その各マスがある各ブロッ ク行･ブロック列の3ブロック間で互いにマス 行･マス列が異なるように数字3が入る空きマ スを､図30の青枠で示します｡ ブロック列Ⅱで､マスa6,マスd4の数字3か ら､マスi5の数字3が確定し､ブロック行Cで､ マスi5の数字3から､マスg8,マスh1の数字3 が確定し､ブロック列Ⅲで､マスb7,マスg8の 数字3から､マスf9の数字3が確定します｡
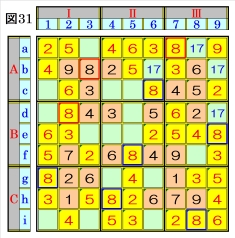	図31で､マスi8は､ブロックCⅢのオンリーワ ンの不足数字であり､マスh4は､マス行hのオ ンリーワンの不足数字であり､また､マスe9 は､マス列9のオンリーワンの不足数字で､それ ぞれ数字8に確定できるので､数字8に着目し て手順①を行います｡ 数字8は､マスa7,マスb3,マスd2,マスe9,マ スh4,マスi8にあるので､その各マスがある各 ブロック行･ブロック列の3ブロック間で互い にマス行･マス列が異なるように数字8が入る 空きマスを､図31の青枠で示します｡ ブロック行Bで､マスd2,マスe9の数字8か ら､マスf5は､数字8に確定し､ブロック行Cで､ マスh4,マスi8の数字8から､マスg1は､数字 8に確定し､ブロック列Ⅱで､マスf5,マスh4 の数字8から､マスc6は､数字8に確定します｡
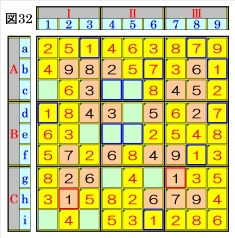	図32で､マスf8は､マス行fのオンリーワンの 不足数字で､数字1に確定できるので､数字1に 着目して手順①を行います｡ 数字1は､マスf8,マスg7,マスh2にあるので､ その各マスがある各ブロック行･ブロック列の 3ブロック間で互いにマス行･マス列が異なる ように数字1が入る空きマスを､図32の青枠で 示します｡ ブロック列Ⅲで､マスf8,マスg7の数字1か ら､マスb9の組数字1,7は､数字1に確定でき､ ブロック行Aで､マスb9とマスc4かマスc5に 入る数字1から､マスa3は､数字1に確定でき､ ブロック列Ⅰで､マスa3,マスh2の数字1か ら､マスd1は､数字1に確定でき､更に､ブロッ ク行Cで､マスg7,マスh2の数字1から､マス i6も､数字1に確定できます｡ 組数字1,7のマスb9が数字1に確定したこと から､組数字1,7のマスa8,マスb6,マスd9 は､数字7に確定できます｡
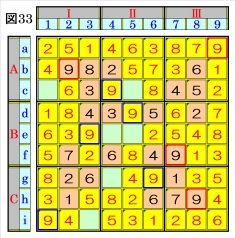	図33で､マスd5は､マス行dのオンリーワンの 不足数字であり､マスe3は､ブロックBⅠのオ ンリーワンの不足数字であり､マスg6は､マス 列6のオンリーワンの不足数字で､それぞれ数 字9に確定できるので､数字9に着目して手順 ①を行います｡ 数字9は､マスa9,マスb2,マスd5,マスe3,マ スf7,マスg6,マスh8にあるので､その各マス がある各ブロック行･ブロック列の3ブロック 間で互いにマス行･マス列が異なるように数字 9が入る空きマスを､図33の青枠で示します｡ ブロック列Ⅰで､マスb2,マスe3の数字9か ら､マスi1は､数字9に確定し､ブロック列Ⅱ で､マスd5,マスg6の数字9から､マスc4は､ 数字9に確定します｡
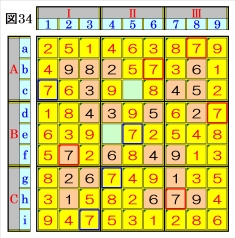	図34で､マスc1は､ブロックAⅠのオンリーワ ンの不足数字であり､マスi3は､ブロックCⅠ のオンリーワンの不足数字であり､マスg4は､ ブロックCⅡのオンリーワンの不足数字で､そ れぞれ数字7に確定できるので､数字7に着目 して手順①を行います｡ 数字7は､マスa8,マスb6,マスc1,マスd9,マ スf2,マスg4,マスh7,マスi3にあるので､そ の各マスがある各ブロック行･ブロック列の3 ブロック間で互いにマス行･マス列が異なるよ うに数字7が入る空きマスを､図34の青枠で示 します｡ ブロック列Ⅱで､マスb6,マスg4の数字7か ら､マスe5は､数字7に確定します｡
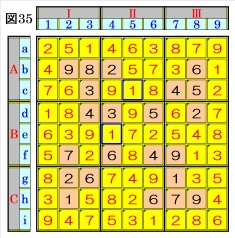	図35で､マスc5,マスe4は､それぞれマス行c, マス行eのオンリーワンの不足数字であること から､それぞれ数字1に確定できます｡ これで､この名人級問題の例のすべての数字が 確定しました｡

　上記のように､手順①～⑤を適宜繰り返すことで､初心者でも､難問が解けてしまいます｡

手順①　各ブロック行･列の3ブロック間の数字配列を､数字1⇒9の順にチェックし､ 　　　　 その数字が入るオンリーワンの空きマスがあれば､その数字に確定する｡  手順③　各空きマスがあるマス行･マス列･ブロック内の全数字1～9をチェックし､ 　　　　 不足数字がオンリーワンの空きマスがあれば､その数字に確定する｡  手順⑤　空きマスに入る候補がオンリーツウの組数字を探して仮決めする｡